Greetings young learners! Today, we will learn about converting binary numbers to hexadecimal numbers. Binary and hexadecimal are both number systems that are used to represent numerical values. Binary uses only two digits - 0 and 1, while hexadecimal uses sixteen digits - from 0 through to F. Understanding how to convert binary numbers to hexadecimal numbers can be an important skill in computer science and engineering.

Binary numbers are numbers that use only two digits: 0 and 1. They are used by computers and other electronic devices to store and process information. Hexadecimal numbers are numbers that use 16 symbols: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E and F. They are used to represent binary numbers in a shorter and more readable way.

To convert a binary number into a hexadecimal number, you need to use a table that shows the equivalent hexadecimal symbol for each group of four binary digits. Here is the table:

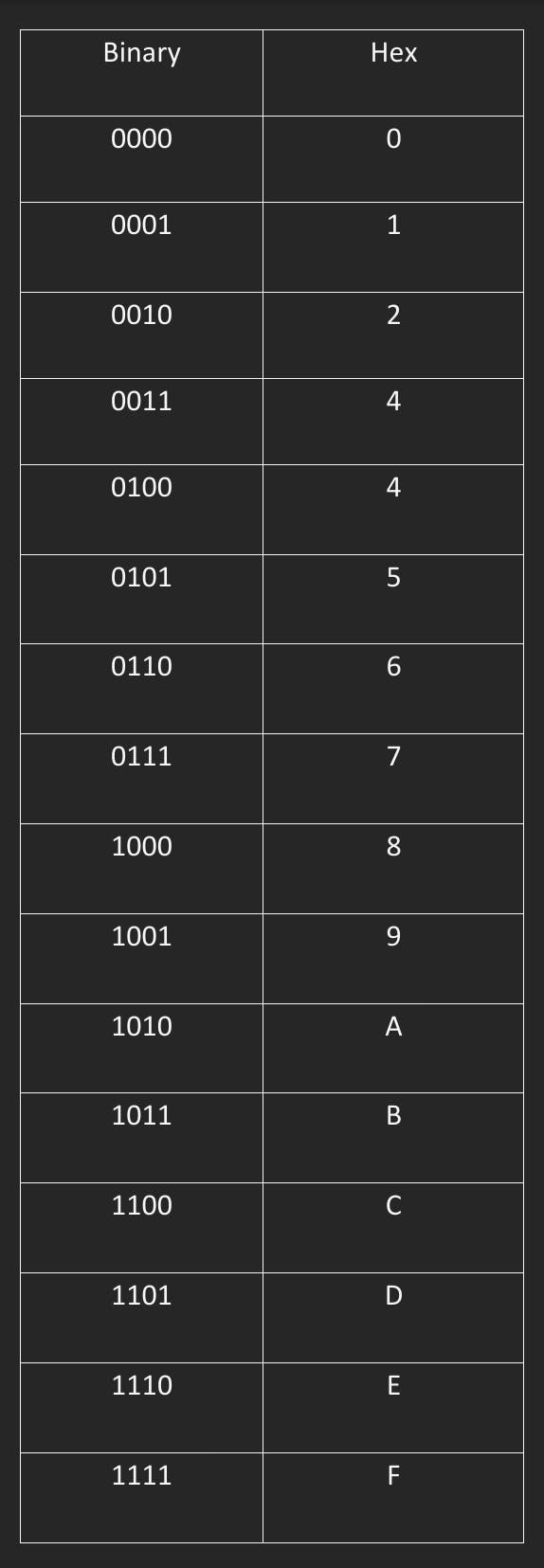
Converting Binary to Hexadecimal

To convert a binary number into a hexadecimal number, follow these steps:

- Starting from the right (the least significant bit), separate your binary number into groups of four digits each.

- Convert each group of four binary digits into the equivalent hexadecimal symbol, using the table above.

- Write the hexadecimal symbols from left to right, without any spaces or commas.

For example, let's convert the binary number `11011001` into a hexadecimal number.

Step 1: Separate the binary number into groups of four digits each.

11011001 -> 1101 , 1001

Step 2: Convert each group of four binary digits into the equivalent hexadecimal symbol.

1101 -> D

1001 -> 9

Step 3: Write the hexadecimal symbols from left to right.

D9

Therefore, the hexadecimal equivalent of 11011001 is D9.

Hopefully, this blog post has helped you understand how to convert binary numbers to decimal numbers. Follow my website if you are interested in learning more about binary numbers and other number systems, I will soon upload other topics as well.